The Recursive Pattern Pathfinder

A fractal algorithm for finding paths by recursively applying line patterns, could this create hyper-fast autorouters?

An example of the recursive pathfinder, read on to see the animation!

There are a lot of benefits to using intersection calculations vs grids for fast autorouters, Grids take up a lot of memory and cause the algorithm to go slower as it routes across more real distance (I discuss this a bit in the intersection-jumping algorithm article). This means that grid-based autorouting algorithms are not scale-invarant, a problem over 100mm will take 10x more compute than a problem over 10mm.

I was trying to think of ways to create an autorouting input/output data format that would be optimal for training machine learning algorithms when I realized that patterns are an incredibly useful way to represent scale-invariant autorouting results. What I mean is that if you could build a classifier that outputs a set of probabilities for a set of predefined routes. This is much easier to “learn” than outputting images or coordinate paths.

3 outputs corresponding to the probability that 3 different paths are possible

There are a lot of benefits to having a constrained output space. The less options to choose from, the less ways to be wrong! I also realized I could now create a very simple algorithm that recursively attempts patterns for any region with a collision.

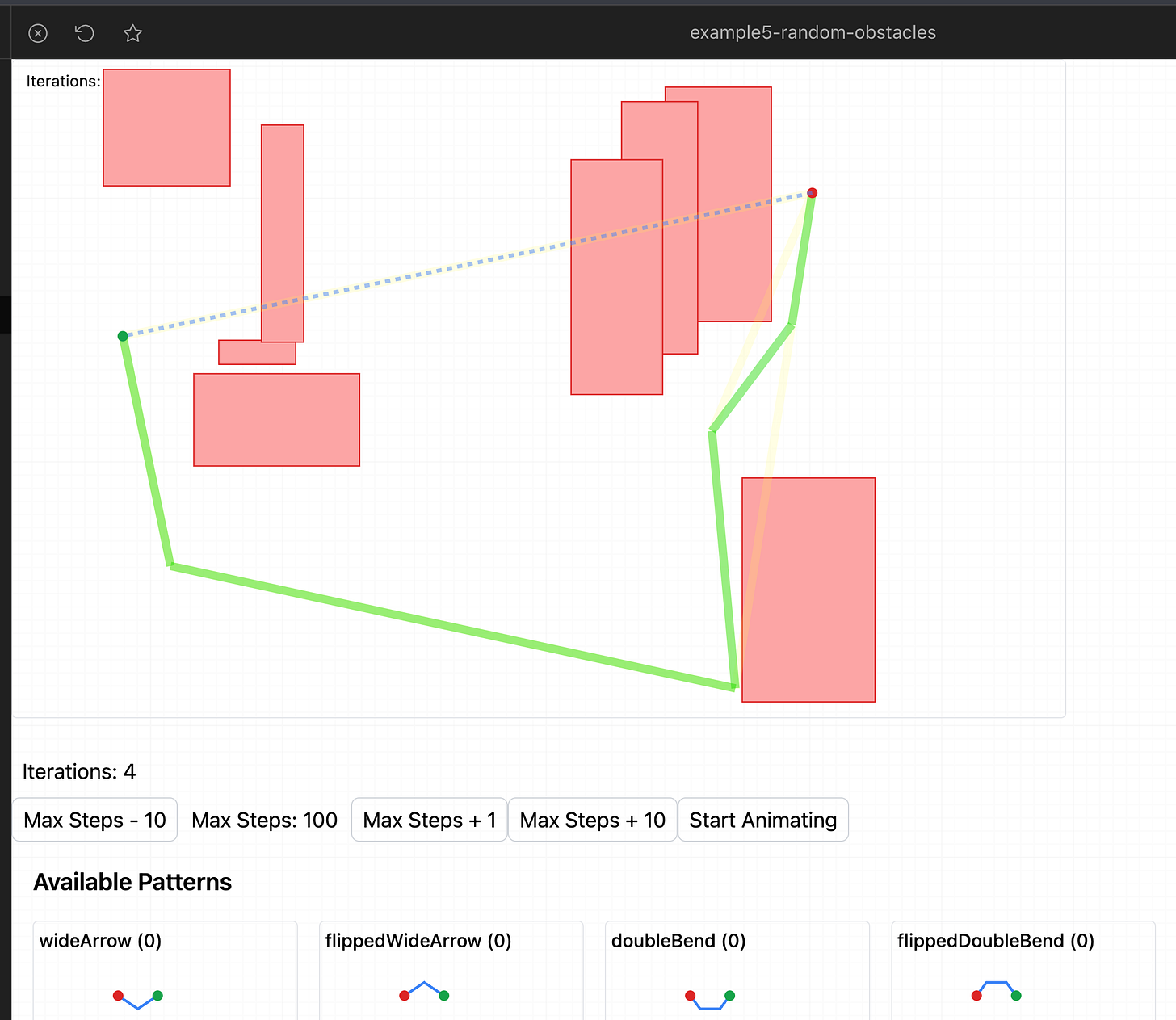
To do this, we just write an algorithm that says “whenever there is an intersection with an obstacle, take the segment that ran into the obstacle and try to replace it with any of the predefined patterns”

Check it out in the short video below!

Can you see what patterns were recursively applied above? There are only 4!

Each of these patterns is applied to each segment that has collisions

This algorithm scales nearly perfectly with the complexity of the autorouting problem (the gray obstacles) so it’s a great choice for sparse problems! I also like how the depth of the recursion is a nice natural measurement for complexity.

It’s also kind of crazy to me that these patterns can actually allow the pathfinder to go backwards

The sky is the limit if you’re recursive enough!

We have a new dataset of keyboard autorouting problems that I’m eager to give it a try on! This will require some “3d patterns” which insert vias. I think this will help to find major issues in the “pattern representation” of traces. Each time you subdivide a line, you increase the number of possible traces that AI will need to classify. A circuit can easily have 3,000 traces, so all of this can add up!

Some of the problems from our new dataset, 2 traces per key!

I’ll report back soon. Until next time!